I will solve a problem similar to one done earlier: how far can a sun-like star be so it is visible to us?
5. The eye needs 10 photons to send a signal to the brain. From Pf Johnson's earlier post on OoM we calcuate the eye's area as .25cm^2 (correspond to an entrance diameter of .5 cm for a fully dilated square-approximation eye). Thus we need to define our sun-like star's distance such that it emits
10 photons/ .25cm^2 =40 photons/cm^2
By this we mean to take star's distance to us, R, and create a sphere of radius R with the sun at the center such that, given the star emits isotropically, we have 40 photons on each cm^2 of the sphere.
Then the total number of photons emitted by the sun's double equals 40 photons/cm^2 *R^2. We want the twin to be just far that we can still see it from a dark site (no light pollution). The energy of a single photon is E_n=h*c//Lambda, were h is Plank's constant and /Lambda~ 550 nm, in the middle of the visible spectrum.
The energy of a single photon h*c/(/lambda))=3.67*10^-12 ergs.
Total energy emitted by sun's double is n*E_n where n is number of photons emitted by sun's double. We can find luminosity from this since we have a time interval. Our eye has a read rate of ~24 fps.
To be visible, luminosity= n*E_n (in ergs)*24 (frames/second).
We know the sun's luminosity is 4*10^33 ergs/s.
4*10^33=n*3.67*10^-12*24, so n=4.5*10^43 photons
But n= 40 photons/cm^2 * 4pi*R^2, and we calculate R=28*10^19cm, or approximately 317ly. The actual distance the sun can be away and still visible is ~100 ly, so this is correct to a factor of 3.
I compared this to Pro Johnson's blog post OoM where he calculated the number of photons to be 10^41 not 10^43. However, Professor Johnson assume read rate of 100 fps not 24, and also reached luminosity 10^33 while I used 4*10^33. That introduces one order of magnitude difference. The 2nd comes because there was a calculation error in OoM calculating the total energy. It should come out to 10^30 not 10^31 erg. But these are all order of magnitude estimations and mistakes, which is why our answer is correct to an OoM.
Saturday, December 3, 2011
Wednesday, November 30, 2011
Reflections on the Interview
This is an immediate follow-up to the previous post with John Pharo's and my interview with Professor Richard Ellis.
Quite a few things surprised me. One of the first things we learned about our interviewee was that at some point Professor Richard wanted to quit astronomy for advertising. Oddly enough, it's reassuring to know that rage-quitting isn't a modern fad and disinterest in a field of astronomy doesn't necessarily convey disinterest in all of astronomy.
In retrospect, he might have been able to get a different PhD thesis other than the tedium of studying solar composition if he had been a bit more assertive, but he felt humbled by the professors in the field. And while pursuing any research it is important to keep the big picture in mind. Where does my research fit into the realm of astronomy? What consequences will it have if true?
The pattern to getting to a research and professorial position involves a lengthy post-doc period of research that often continues after you get your professorial position. Pro Richard had worked quite a few years on searching for supernova, and much of that time with the Supernova Cosmological Project. Perlmutter, who shared the Nobel Prize for explaining the expansion of the universe, had spent much of the last 20 years on the same project. But Pro Richard pointed that you had to balance personal content into the equation, which is why he prefers to take on several varied project over the same course of time.
What was perhaps the most illuminating story was the initially misguiding conclusion that the universe was actually decelerating. After only a sample size of 8 supernovae (several of which are type 1b and not standard candles, and only a couple were appropriate for the study), it seemed that the universe was actually slowing in its expansion. After using a sampling of 50 supernovae, the SCP team published a paper on their conclusion that the universe was indeed accelerating in expansion. This is particularly significant to us for 2 reasons. It would be mind-rattling to publish a paper you were convinced was onto something, only to publish the polar argument a few years later. Second, such an argument of expansion came as a surprise to many in the scientific community, so the charisma and confidence of advocators was important in persuading the community.
Career-wise, Pro Ellis felt that while astronomy was still a strong field, biology was the fastest growing current field. I was especially intrigued by his relative laxness to submitting research proposals and his willingness to engage in a variety of subtopics in astronomy. Variety is a pleasant alternative to the indecision in career paths I'm facing. Especially pleasant was the distinction between the avid proposal printing astronomer early in the career, with the more composed, content, and curious astronomer later in the career.
Some useful addenda: Professor Richard Ellis is an observational cosmologist known for his work in supernova, universe expansion, and dark matter. He also has a wikipedia article.
For some really interesting reading, check out Science and Philosophy, a 2007 interview of Professor Richard Ellis by a history of science graduate student. Professor Ellis ended his interview with us almost exactly, talking about how emails were rare and most communication was with telexes back in the 80's.
I wanted to say a few words about his distinctions between the US and Europe (the land of hermit scientists) but John's Blog covers it well.
Quite a few things surprised me. One of the first things we learned about our interviewee was that at some point Professor Richard wanted to quit astronomy for advertising. Oddly enough, it's reassuring to know that rage-quitting isn't a modern fad and disinterest in a field of astronomy doesn't necessarily convey disinterest in all of astronomy.
In retrospect, he might have been able to get a different PhD thesis other than the tedium of studying solar composition if he had been a bit more assertive, but he felt humbled by the professors in the field. And while pursuing any research it is important to keep the big picture in mind. Where does my research fit into the realm of astronomy? What consequences will it have if true?
The pattern to getting to a research and professorial position involves a lengthy post-doc period of research that often continues after you get your professorial position. Pro Richard had worked quite a few years on searching for supernova, and much of that time with the Supernova Cosmological Project. Perlmutter, who shared the Nobel Prize for explaining the expansion of the universe, had spent much of the last 20 years on the same project. But Pro Richard pointed that you had to balance personal content into the equation, which is why he prefers to take on several varied project over the same course of time.
What was perhaps the most illuminating story was the initially misguiding conclusion that the universe was actually decelerating. After only a sample size of 8 supernovae (several of which are type 1b and not standard candles, and only a couple were appropriate for the study), it seemed that the universe was actually slowing in its expansion. After using a sampling of 50 supernovae, the SCP team published a paper on their conclusion that the universe was indeed accelerating in expansion. This is particularly significant to us for 2 reasons. It would be mind-rattling to publish a paper you were convinced was onto something, only to publish the polar argument a few years later. Second, such an argument of expansion came as a surprise to many in the scientific community, so the charisma and confidence of advocators was important in persuading the community.
Career-wise, Pro Ellis felt that while astronomy was still a strong field, biology was the fastest growing current field. I was especially intrigued by his relative laxness to submitting research proposals and his willingness to engage in a variety of subtopics in astronomy. Variety is a pleasant alternative to the indecision in career paths I'm facing. Especially pleasant was the distinction between the avid proposal printing astronomer early in the career, with the more composed, content, and curious astronomer later in the career.
Some useful addenda: Professor Richard Ellis is an observational cosmologist known for his work in supernova, universe expansion, and dark matter. He also has a wikipedia article.
For some really interesting reading, check out Science and Philosophy, a 2007 interview of Professor Richard Ellis by a history of science graduate student. Professor Ellis ended his interview with us almost exactly, talking about how emails were rare and most communication was with telexes back in the 80's.
I wanted to say a few words about his distinctions between the US and Europe (the land of hermit scientists) but John's Blog covers it well.
An Interview with Professor Richard Ellis
John and I interviewed Professor Richard Ellis this Monday. He had just returned from a ski trip in Big Bear (it's snowing there already!)
I will try to restrict only to the questions I asked but will also add some of John's questions to provide context. This is not scripted, I am constructing from notes and memory. I will maintain first and second tense use because it sounds neater.
(John): Could you tell us a bit about your early education and what lead you to your career path?
My case is a rare one in astronomy. I was into astronomy since I was 6, I built a telescope in high school, and went off to the University of Durham knowing full well I wanted to do astronomy. I always wanted to stay in academia. After a bachelor's I continued for a PhD but was quickly disillusioned. I was stuck studying the composition of the sun to high precision via transmission strength, and it was very boring and tedious. I enjoyed larger scale observational cosmology.
So after getting my PhD, I decided to quit astronomy and get a real job. I applied for computing, advertising, and editing (Nature) positions. I got the advertising position and was getting ready to move when I realized, at the last minute, I didn't want to quit astronomy.
(The following are my questions)
In the 1980's you had to struggle with funding for the Supernova Cosmology Project. How is it like juggling research with funding proposals?
It was initially just 4 of us searching for supernova. We used an observatory in Chile so once a month one of use would have to go and sift through the data. Perlmutter joined us and had the idea of attaching a camera to the telescope with more pixels so we could see through a patch of sky, one large enough to guarantee at least one supernova. Our project got bigger then and we starting finding more supernova. The problem was none of them were as far away as the one we had found earlier on, and funding became tight. I had to travel around quite a bit to insure funding.
Now searching for funding is definitely more time-consuming, especially so given the economy. I am not very ambitious and have only a small group with no post-docs because they're expensive. You can also keep moving because each time you start working somewhere new you get a big starting package.
We're particularly interested in doing SURFs this summer as undergraduates. How would you identify a good researcher?
A good researcher has to conceive the important idea, and avoid the danger of gathering data without understanding it. It's a big picture goal.
It's also the topics you choose in research. The most exciting projects are the ones that are just feasible science and skirt the edges of what we know. You need vision and determination to get a lasting result.
Collaboration and generosity is also important. Will the professor share his brightest idea with a student to work on and publish a paper on? Sometimes I've had student researchers encourage me to take a particular project on.
There's a big jump to becoming a graduate student. You don't have classes or tests. You have to learn to be independent at this point when working on projects, and I try to introduce my graduate students to that early on.
To be a good scientist and not just a good researcher you need charisma and eloquence. You have to publicize your work, engage the audience with your enthusiasm so they understand why what you're researching is interesting and deserves funding.
We visited Palomar the beginning of the year...
That's great! How was your trip?
....It was quirky and interesting. We saw the rubber ducks and gloves used to mark important features there. You were the director at Palomar and you've also worked in observatories in England, Chile, and Australia. Have you seen anything like that there?
No, I can't say I have. That's unique to the environment here.
I know I want to do astronomy but I'm not sure what field I want to specialize in. What's your advice?
I should add a few things about career paths. I've swapped my research interests quite a bit. I like to pursue a variety of research topics at once. I've done solar composition, supernovae extensively, dark matter recently. That's not to say I've jumped over to, say biology. But I do know a couple physicists who have jumped boat and became biologists. I guess biology doesn't have enough physicists. You're not at all limited to a single of interest as astronomers. I'm sure if I had been more assertive, I wouldn't have ended up with studying the composition of the sun for my PhD.
Well that's all the questions I have, and I think we covered all we intended to.
Did you have the stone etched with the gravitational const...
You mean the cosmological constant?
Yes, yes of course. Slip of tongue.
I did, in Peru. I asked this stonecarver in a street fair if he could carve Greek symbols and he said yes. So I told him to carve \Lambda = 0. I realized what I had done later and took the stone back and asked him if he could draw a line through the equal sign! He did and it was mailed to me a bit later.
Next to that I have this small holographic projection of a piece of the universe. It's amazing how they can 3-dimensionally project that in glass. I still don't know how they do it.
I will try to restrict only to the questions I asked but will also add some of John's questions to provide context. This is not scripted, I am constructing from notes and memory. I will maintain first and second tense use because it sounds neater.
(John): Could you tell us a bit about your early education and what lead you to your career path?
My case is a rare one in astronomy. I was into astronomy since I was 6, I built a telescope in high school, and went off to the University of Durham knowing full well I wanted to do astronomy. I always wanted to stay in academia. After a bachelor's I continued for a PhD but was quickly disillusioned. I was stuck studying the composition of the sun to high precision via transmission strength, and it was very boring and tedious. I enjoyed larger scale observational cosmology.
So after getting my PhD, I decided to quit astronomy and get a real job. I applied for computing, advertising, and editing (Nature) positions. I got the advertising position and was getting ready to move when I realized, at the last minute, I didn't want to quit astronomy.
(The following are my questions)
In the 1980's you had to struggle with funding for the Supernova Cosmology Project. How is it like juggling research with funding proposals?
It was initially just 4 of us searching for supernova. We used an observatory in Chile so once a month one of use would have to go and sift through the data. Perlmutter joined us and had the idea of attaching a camera to the telescope with more pixels so we could see through a patch of sky, one large enough to guarantee at least one supernova. Our project got bigger then and we starting finding more supernova. The problem was none of them were as far away as the one we had found earlier on, and funding became tight. I had to travel around quite a bit to insure funding.
Now searching for funding is definitely more time-consuming, especially so given the economy. I am not very ambitious and have only a small group with no post-docs because they're expensive. You can also keep moving because each time you start working somewhere new you get a big starting package.
We're particularly interested in doing SURFs this summer as undergraduates. How would you identify a good researcher?
A good researcher has to conceive the important idea, and avoid the danger of gathering data without understanding it. It's a big picture goal.
It's also the topics you choose in research. The most exciting projects are the ones that are just feasible science and skirt the edges of what we know. You need vision and determination to get a lasting result.
Collaboration and generosity is also important. Will the professor share his brightest idea with a student to work on and publish a paper on? Sometimes I've had student researchers encourage me to take a particular project on.
There's a big jump to becoming a graduate student. You don't have classes or tests. You have to learn to be independent at this point when working on projects, and I try to introduce my graduate students to that early on.
To be a good scientist and not just a good researcher you need charisma and eloquence. You have to publicize your work, engage the audience with your enthusiasm so they understand why what you're researching is interesting and deserves funding.
We visited Palomar the beginning of the year...
That's great! How was your trip?
....It was quirky and interesting. We saw the rubber ducks and gloves used to mark important features there. You were the director at Palomar and you've also worked in observatories in England, Chile, and Australia. Have you seen anything like that there?
No, I can't say I have. That's unique to the environment here.
I know I want to do astronomy but I'm not sure what field I want to specialize in. What's your advice?
I should add a few things about career paths. I've swapped my research interests quite a bit. I like to pursue a variety of research topics at once. I've done solar composition, supernovae extensively, dark matter recently. That's not to say I've jumped over to, say biology. But I do know a couple physicists who have jumped boat and became biologists. I guess biology doesn't have enough physicists. You're not at all limited to a single of interest as astronomers. I'm sure if I had been more assertive, I wouldn't have ended up with studying the composition of the sun for my PhD.
Well that's all the questions I have, and I think we covered all we intended to.
Did you have the stone etched with the gravitational const...
You mean the cosmological constant?
Yes, yes of course. Slip of tongue.
I did, in Peru. I asked this stonecarver in a street fair if he could carve Greek symbols and he said yes. So I told him to carve \Lambda = 0. I realized what I had done later and took the stone back and asked him if he could draw a line through the equal sign! He did and it was mailed to me a bit later.
Next to that I have this small holographic projection of a piece of the universe. It's amazing how they can 3-dimensionally project that in glass. I still don't know how they do it.
Wednesday, November 23, 2011
Virializing the Night Away #4
By David Vartanyan
Coauthors: Mee and John
4) In this problem we will show that the sun would rapidly collapse under its own weight if there were no pressure countering the collapse. We will introduce degeneracy pressure as a dominant pressure countering collapse.
a. The rate at which the sun generates energy is defined as the sun's luminosity L_s, 3.9*10^33 erg/s.
b. Assume the sun is powered entirely by fusion with a 0.7% efficiency, and that fusion occurs only in the sun's core which is 10% of the solar mass.
Then, defining M_s as the solar mass we have the total energy available to the sun:
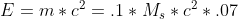
=1.2*10^51 ergs.
The sun will burn out at time t = E/L_s, the sun's total energy divided by the luminosity (rate of energy consumption), so:
t= 9.9 billion years
The more massive a star, the more energy it has available to burn through and the longer it typically stays on the main sequence.
We initially tried to find the total energy by summing all the individual reactions that occurred. We considered the total number of fusion reactions in the core multiplied by the energy released in each reaction. For a core with n hydrogen atoms available for fusion, there will be n fusion reactions
4 1H + 2 e -->; 4He + 2 neutrinos + 6 photons (Fusion Steps)
which each release 26 MeV. The sun's core is .1 M_s. Dividing the core's mass by the mass of a hydrogen atom (assuming it consists of only hydrogen before fusion has begun), we have
n= 1.2*10^56, so total energy is n*26MeV = 5*10^51 ergs
c. We solve this similarly to the problem of an elliptical orbit with eccentricity of one rather than integrating over the sun's surface to calculate collapse. Define the sun so that it is free-falling towards the core. Label the core as one focus of the ellipse and a point on the sun's surface as the other focus. Assuming the sun is a uniform homogenous sphere, all points on the surface should have the same 'period' of collapse.
From Kepler's third law:
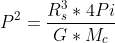
where R_s is the sun's core radius (.25* sun's radius), M_c is the mass of the sun's core (M_c=.1*M_s),
The time for collapse for an eccentricity 1 orbit is half the period.
This comes to about 31 minutes (Nathan's group got 24 minutes using a slightly different radius). That is quite fast.
d. After some initial collapse, degeneracy pressure becomes significant in countering core collapse. Degeneracy pressure is an extension of the Pauli exclusion principle: 2 electrons won't occupy same quantum state so after some collapse this degeneracy pressure takes effect. When particle spacing is on the order of the de Broglie wavelength
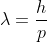
degeneracy pressure becomes significant. Assuming the particles velocities are roughly the same, electrons have a much smaller mass so they have a larger de Broglie wavenelength.
More rigorously, kinetic energy scales as k*T where T is the temperature at the sun's core. So mv^2~T and v~Sqrt(T/m).
A 2-D image of the spacing of degeneracy pressure:
For an electron in the sun's core:
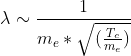
For proton:
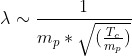
At the same temperature, electron wavelengths near the de Broglie limit scale with the inverse square root of electron mass, and proton wavelengths with the inverse square root of proton mass. Since an electron is much less massive than a proton, electrons have a larger de Broglie wavelength.
Therefore electrons reach their critical density first. For a system (like our sun) dominated by hydrogen such that electrons and protons are roughly equal, electron degeneracy pressure dominates over proton degeneracy pressure.
In the case where the star's density is too high for degeneracy to support, we have a black hole!
e. Degeneracy becomes important at an electron number density ~
, with mass density scaling as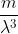 
where m is the mass of a hydrogen atom.
In terms of fundamental units, mass density becomes important at the de Broglie wavelength, or when mass density ~
Since \lambda ~ h/p ~h/(m_e*v) and 1/2 m_e*v^2 =3/2 k*T for n = 1 (a single electron in a core at critical density), so v~ Sqrt(3k*T/m_e).
mass density ~ m_H/(\lambda^3)~m_H*p^3/h^3~m_h*(m_e)^3*v/h^3. Substituting for velocity gives us the mass density equation above.
According to Wolfram-Alpha, the density of the sun's core is around 150g/cm^3 (approximate by density = mass/volume = .1 * solar mass/(4*pi*.25 solar radius^3).
Find \lambda at the sun's core temperature T_c = 1.5*10^7 K.
This comes out to be around 80 g/ cm^3, half of the actual value. Before we claim content with an OoM estimate, consider sources of inaccuracy. The sun's density isn't uniform, we likely have some other unknown quantum effects at this scale, the sun's temperature isn't uniform, we have some proton degeneracy contribution (but very, very little), and critical density itself is an OoM equation.
Now we can be content.
-------------------------------------------------
Thanks to John and Mee for their cooperation, and to Professor Johnson for pointing out that the reason we were getting critical density to be higher than is possible given all the particles in the universe was that we were using the sun's mass to find mass density rather than the mass of a hydrogen atom.
Coauthors: Mee and John
4) In this problem we will show that the sun would rapidly collapse under its own weight if there were no pressure countering the collapse. We will introduce degeneracy pressure as a dominant pressure countering collapse.
a. The rate at which the sun generates energy is defined as the sun's luminosity L_s, 3.9*10^33 erg/s.
b. Assume the sun is powered entirely by fusion with a 0.7% efficiency, and that fusion occurs only in the sun's core which is 10% of the solar mass.
Then, defining M_s as the solar mass we have the total energy available to the sun:
=1.2*10^51 ergs.
The sun will burn out at time t = E/L_s, the sun's total energy divided by the luminosity (rate of energy consumption), so:
t= 9.9 billion years
The more massive a star, the more energy it has available to burn through and the longer it typically stays on the main sequence.
We initially tried to find the total energy by summing all the individual reactions that occurred. We considered the total number of fusion reactions in the core multiplied by the energy released in each reaction. For a core with n hydrogen atoms available for fusion, there will be n fusion reactions
4 1H + 2 e -->; 4He + 2 neutrinos + 6 photons (Fusion Steps)
which each release 26 MeV. The sun's core is .1 M_s. Dividing the core's mass by the mass of a hydrogen atom (assuming it consists of only hydrogen before fusion has begun), we have
n= 1.2*10^56, so total energy is n*26MeV = 5*10^51 ergs
c. We solve this similarly to the problem of an elliptical orbit with eccentricity of one rather than integrating over the sun's surface to calculate collapse. Define the sun so that it is free-falling towards the core. Label the core as one focus of the ellipse and a point on the sun's surface as the other focus. Assuming the sun is a uniform homogenous sphere, all points on the surface should have the same 'period' of collapse.
From Kepler's third law:
where R_s is the sun's core radius (.25* sun's radius), M_c is the mass of the sun's core (M_c=.1*M_s),
The time for collapse for an eccentricity 1 orbit is half the period.
This comes to about 31 minutes (Nathan's group got 24 minutes using a slightly different radius). That is quite fast.
d. After some initial collapse, degeneracy pressure becomes significant in countering core collapse. Degeneracy pressure is an extension of the Pauli exclusion principle: 2 electrons won't occupy same quantum state so after some collapse this degeneracy pressure takes effect. When particle spacing is on the order of the de Broglie wavelength
degeneracy pressure becomes significant. Assuming the particles velocities are roughly the same, electrons have a much smaller mass so they have a larger de Broglie wavenelength.
More rigorously, kinetic energy scales as k*T where T is the temperature at the sun's core. So mv^2~T and v~Sqrt(T/m).
A 2-D image of the spacing of degeneracy pressure:
For an electron in the sun's core:
For proton:
At the same temperature, electron wavelengths near the de Broglie limit scale with the inverse square root of electron mass, and proton wavelengths with the inverse square root of proton mass. Since an electron is much less massive than a proton, electrons have a larger de Broglie wavelength.
Therefore electrons reach their critical density first. For a system (like our sun) dominated by hydrogen such that electrons and protons are roughly equal, electron degeneracy pressure dominates over proton degeneracy pressure.
In the case where the star's density is too high for degeneracy to support, we have a black hole!
e. Degeneracy becomes important at an electron number density ~
, with mass density scaling as where m is the mass of a hydrogen atom.In terms of fundamental units, mass density becomes important at the de Broglie wavelength, or when mass density ~
Since \lambda ~ h/p ~h/(m_e*v) and 1/2 m_e*v^2 =3/2 k*T for n = 1 (a single electron in a core at critical density), so v~ Sqrt(3k*T/m_e).
mass density ~ m_H/(\lambda^3)~m_H*p^3/h^3~m_h*(m_e)^3*v/h^3. Substituting for velocity gives us the mass density equation above.
According to Wolfram-Alpha, the density of the sun's core is around 150g/cm^3 (approximate by density = mass/volume = .1 * solar mass/(4*pi*.25 solar radius^3).
Find \lambda at the sun's core temperature T_c = 1.5*10^7 K.
This comes out to be around 80 g/ cm^3, half of the actual value. Before we claim content with an OoM estimate, consider sources of inaccuracy. The sun's density isn't uniform, we likely have some other unknown quantum effects at this scale, the sun's temperature isn't uniform, we have some proton degeneracy contribution (but very, very little), and critical density itself is an OoM equation.
Now we can be content.
-------------------------------------------------
Thanks to John and Mee for their cooperation, and to Professor Johnson for pointing out that the reason we were getting critical density to be higher than is possible given all the particles in the universe was that we were using the sun's mass to find mass density rather than the mass of a hydrogen atom.
Saturday, November 19, 2011
Lighter than Air
I'll be the last person to cite a yawhoo (sic) news article, but that's where I read about this: World's Lightest Solid
In the summer of 2009 before entering Caltech I went to D.C for some congressional seminar. During a tour of the city two friends and I ditched the group and headed to the Smithsonian Air n Space Museum. I'd heard about aerogel, and I knew the museum had it on display so I was itching to see it. It looks so ethereal:
silica-based frozen smoke
It's particularly useful in space missions when you want to bring back airtight samples in a zero gravity environment. You can trap space dust which would otherwise vaporise in a solid medium and pass through a gaseous one. Aerogel seemed like the Goldilocks zone between solid and gas.
a star dust collector with aerogel blocks
The Smithsonian sample was developed in JPL earlier on and had 3 times the density of air; current samples are less dense than air, some as low as 43% of the density of air. (But these technically aren't 'aerogels' because they are composed of nanotubes and not a dendritic lattice with evenly spaced pores) Aerogel can be structurally very diverse, consisting of 99.9% air.
It is constructed by surrounding the material mass with an impermeable film and flooding it with light gases like hydrogen and helium, or pump out the air in the material to create vacuums within the structures.
Structurally aerogels are very porous and either are crosslinked polymers all looped together or dendritic polymers branching outwards.
Aerogels can easily shatter (friable) but are incredibly strong structurally and can support up to 1000 times their weight. Since they are so light, this is still less than an atmosphere which is why squeezing it will shatter the cube.
The yawho? article really a distinction between monolithic aerogels and carbon nanotube aerogels (what the article means by an Eiffel tower structure). The stronger, less dense aerogels are made of carbon nanotubes so the lattice structure is more organized than dendritic aerogel, which is weaker by virtue of its random structure.
P.S read the image tag in the article! Caltech worked to develop this new model
P.P.S as best as I could understand it by monolithic structure purists mean aerogel has a singular dendritic structure, while the nanotube structures consist of multiple carbon cylinders woven together. In this case, aerogel is 'cut' off a single stone of chemical building material
In the summer of 2009 before entering Caltech I went to D.C for some congressional seminar. During a tour of the city two friends and I ditched the group and headed to the Smithsonian Air n Space Museum. I'd heard about aerogel, and I knew the museum had it on display so I was itching to see it. It looks so ethereal:
silica-based frozen smoke
It's particularly useful in space missions when you want to bring back airtight samples in a zero gravity environment. You can trap space dust which would otherwise vaporise in a solid medium and pass through a gaseous one. Aerogel seemed like the Goldilocks zone between solid and gas.
a star dust collector with aerogel blocks
The Smithsonian sample was developed in JPL earlier on and had 3 times the density of air; current samples are less dense than air, some as low as 43% of the density of air. (But these technically aren't 'aerogels' because they are composed of nanotubes and not a dendritic lattice with evenly spaced pores) Aerogel can be structurally very diverse, consisting of 99.9% air.
It is constructed by surrounding the material mass with an impermeable film and flooding it with light gases like hydrogen and helium, or pump out the air in the material to create vacuums within the structures.
Structurally aerogels are very porous and either are crosslinked polymers all looped together or dendritic polymers branching outwards.
Aerogels can easily shatter (friable) but are incredibly strong structurally and can support up to 1000 times their weight. Since they are so light, this is still less than an atmosphere which is why squeezing it will shatter the cube.
The yawho? article really a distinction between monolithic aerogels and carbon nanotube aerogels (what the article means by an Eiffel tower structure). The stronger, less dense aerogels are made of carbon nanotubes so the lattice structure is more organized than dendritic aerogel, which is weaker by virtue of its random structure.
P.S read the image tag in the article! Caltech worked to develop this new model
P.P.S as best as I could understand it by monolithic structure purists mean aerogel has a singular dendritic structure, while the nanotube structures consist of multiple carbon cylinders woven together. In this case, aerogel is 'cut' off a single stone of chemical building material
Subscribe to:
Posts (Atom)