Calculating an Astronomical Unit

Main Author: David Vartanyan
Co-authors: John Pharo and Mee Wong-u

Abstract: We will attempt to find the distance between Earth and the sun, an astronomical unit, AU. For our purposes we will assume that an AU is equivalent to the semi-axis of Earth's orbit. Also assume that the sun's angular diameter is 0.5 degrees (half a thumb width approximately). We will also take for simplicity a low-orbit satellite to be in in contact with Earth's surface, radius r_o away from its center.

Introduction:
We extended the arc of the sun in our handout to form an entire circular sun. Then, we studied the periodic movement of Mercury across the surface of the sun. What we were actually seeing was a parallax effect resulting from the movement of the low-orbit satellite as it moved between the poles of the earth. By measuring the ratio of the peaks and troughs of the satellite's orbit to the diameter of the sun, we estimated the ratio of the angular diameter, /alpha, of Mercury's apparent oscillations.

We complete the circle of the sun and measure its diameter as around 20cm. The distance between peaks/troughs of Hg's 'oscillation' is 2mm, so:
 
 and /alpha = .005 degrees, or 8.73e^-5 radians.

There was some controversy as to how we could define the angle subtended by Mercury's 'oscillations'. Initially our group was thinking of defining /beta as this half angle; however /beta gives half the angular diameter of mercurcy as seen from the sun.

Then we tried to define \theta as half the angle subtended by this motion. However we threw out this idea because /theta is equivalent to the angle formed between the line sight of the satellite and a tangent to earth's surface at the location of the satellite, and this fixes Mercury with respect to a distant star.
Rather, since the problem is dependent on the parallax in the Earth-Mercuy-Sun arrangement, we decided to fix the sun relative to Mercury and Earth, assuming without loss of generality that their centers are aligned, and defined /alpha as the twice the angle between the satellite's line of sight and a line connecting all 3 centers.

Calculations:

For our angle measurements (using small angle approximation for /beta and /theta) we have:

From our diagram you can see a triangle formed by these angles or their complements.

We have angle equivalence:

  or 
We now explicitly define lengths:

where a_0 is the astronomical unit, a_H_g is the (mean) distance from Mercury to the sun, and \delta a is their difference, the distance from Earth to Mercury.

Substituting in our angle definitions into our angle equivalence and solving for \delta a, we get :


 after substituting this into our length definition.

By assuming Kepler's third law for Earth and Mercurcy, we get:

where the constants have canceled in the ratio. T_o is 365 days and T_H_g is 87 days (we can keep period in days rather than seconds since their units cancel). Substituting in our relation between a_o and a_H_g and solving for a_o, we have:

 

and a_o 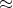9*10^12 cm. An actual astronomical unit is around 1.5*10^13 cm.

 We can calculate the sun's mass to by using Kepler's 3rd Law again but without constructing a ratio:


where M_s is the solar mass and G is the gravitational constant. We have neglected the mass of the earth because it is diminutive to that of the sun. Using the calculated value of the astronomical unit, we calculate M_s to be 4.4*10^29kg. An actual solar mass is about 2*10^30kg.
Defining our solar mass as about 0.2 of an actual solar mass,

we can easily prove by induction that the sun is massless.

Conclusions: The error in our calculated solar mass is due mainly to our approximation of an AU. However, Kepler's Law is also not an exact approach here because we assume that our distance to the sun is along the semi-major axis. But OoM.

Acknowledgements: I used Botox for encoding the equations and a personal scanner to upload my
picture. In drawing the pictures I used a #9 pencil on a 11.5x8.5 sheet of blank paper. The paper was acquired in a ream of 100 sheets from within a box containing 3 reams obtained from Office Depot. My ability to draw rudimentary geometric shapes was acquired over time from unclear sources.